前回、診断検査における以下のような指標について情報を整理していきました。
・真陽性/真陰性
・偽陽性/偽陰性
・感度/特異度
・陽性的中度/陰性的中度
・有病率
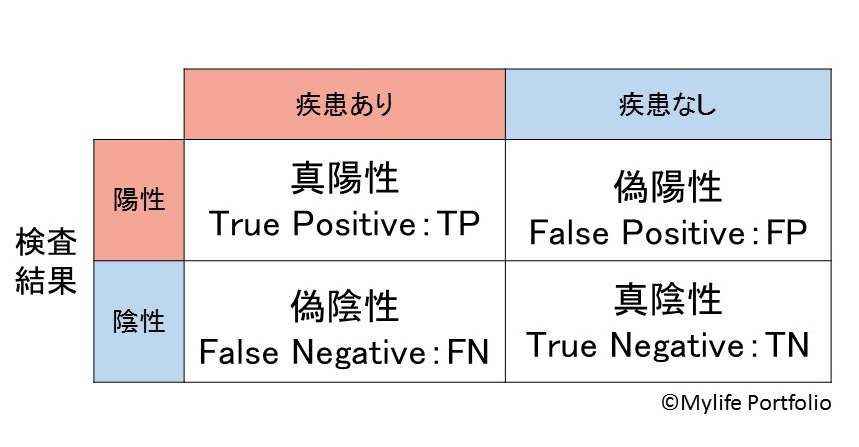
上の表を見ながら、上記の指標の意味や求め方が分かるようであれば問題なく今回の投稿を読み進められるはずです。
怪しい方は、前回の投稿を読んで再確認してもらえると助かります苦笑
前回は、感度・特異度の限界として「的中度は有病率に左右される」という点を紹介させて頂きました。
もちろん、その限界を変わったうえで感度・特異度の情報を利用すれば問題はありません。
しかし、診断検査に関わる指標は他にも存在します。
今回は、尤度比・診断オッズ比という指標について考えていきたいと思います。
ちなみに、尤度比←この漢字、読み方分かりますか? 私は読めませんでした苦笑
私はPT/ATであり、医学的な診断を下せる立場ではありません。様々な検査を元に医学的な診断を下すのは医師の業務(医業)であり、PT/ATが実施できる業務ではありません。
今回の投稿は、あくあでも医師と共通言語を持ち医学的な検査に対する理解を深める為の情報整理である事を御理解下さい。
尤度比とは
尤度比とは、「ゆうどひ」と読みます。
尤とは「尤も(もっとも)」とも読み、尤度比とは「もっともらしさ」を比較したものと言えるかもしれません。
・・・よく分かりませんね苦笑
とりあえず、診断検査の分野で重要となる陽性尤度比・陰性尤度比について説明していきたいと思います。
陽性尤度比とは
陽性尤度比(positive likelihood ratio:+LR)とは
疾患のある者が疾患の無い者と比べて、検査で何倍陽性となりやすいか
という値だと理解して下さい。

上の表から陽性尤度比を求める数式を考え変形させていくと、感度/(1-特異度)という数式によって陽性尤度比が求められることが分かります。
陰性尤度比とは
陰性尤度比(negative likelihood ratio:-LR)とは
疾患のある者が疾患の無い者と比べて、検査で何倍陰性となりやすいか
という値だと理解して下さい。

上の表から陰性尤度比を求める数式を考え変形させていくと、(1-感度)/特異度という数式によって陰性尤度比が求められることが分かります。
詳しい計算や照明は省きますが、尤度比は有病率に左右されない値です。
そのため、診断検査の有効性を表す指標として様々な研究報告の中で用いられています。
尤度比の活用方法
・陽性尤度比が大きければ確定診断に使える
・陰性尤度比が小さければ除外診断に使える
このようなイメージが沸けば、ここまでの理解は十分だと思います。
しかし、感度・特異度のように日常で慣れ親しんだ100%表示の割合の指標ではない為、尤度比はいまいちピンと来ない指標です。
では、ここから尤度比をどう活用していくのか説明していきましょう。
実は、尤度比を用いると「検査前の診断確率」から「検査後の診断確率」を求める事が出来ます。
例題)検査前の状態で疾患を有する確率が30%で陽性尤度比4.13の検査で陽性だった場合、検査後の状態で疾患を有する確率は?
このような場合、以下の手順で検査後の診断確率を求める事ができます。
1. 検査前の確率をオッズに変換
2. 検査前オッズに尤度比をかけて検査後オッズを求める
3. 検査後オッズを検査後の確率に変換
という手順を踏む事で、検査後の診断確率が64%だと明らかにすることが出来ます!
・・・いきなりオッズという言葉が出てきて訳が分かりませんね苦笑
その理論背景は後で説明しますが、頭が混乱してしまうので、ここでは割愛します!
めんどくさい計算手順を踏む事で、尤度比から検査後の診断確率を求める事が出来るという事を理解して頂ければ十分です。
計算自体は難しいものではないので、Excelで簡単に計算シートを作る事は可能です。
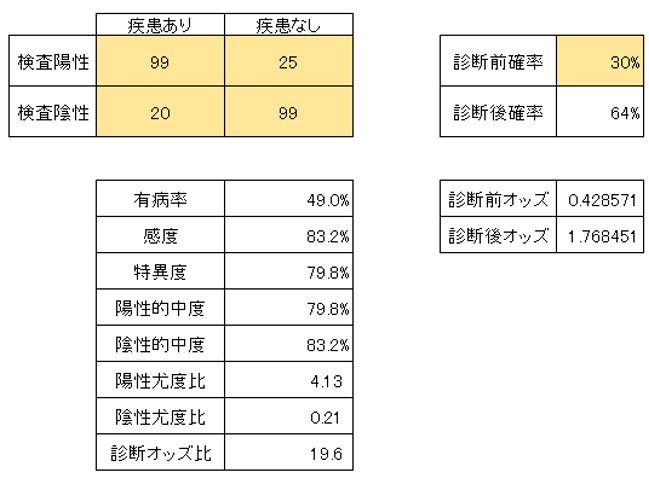
ただ、いちいち計算するのが手間になるのは否めません。
そこで、先人は尤度比による診断確率の変化を視覚的に理解できる便利なツールを作り出しました。
1975年にTJ faganがDr.Katz'sの論文に対するLatterの中で、以下のノモグラム(計算図表)を紹介している。
T J Fagan. Letter: Nomogram for Bayes theorem . N Engl J Med. 1975 Jul 31;293(5):257.(論文要約)
左側の軸:検査後に疾患を有している確率
中央の軸:尤度比
右側の軸:検査前に疾患を有している確率
このノモグラムは、3者を直線で結ぶ事が出来るというものである。
先ほどの例題を、このノモグラムに当てはめてみましょう。
例題)検査前の状態で疾患を有する確率が30%で陽性尤度比4.13の検査で陽性だった場合、検査後の状態で疾患を有する確率は?
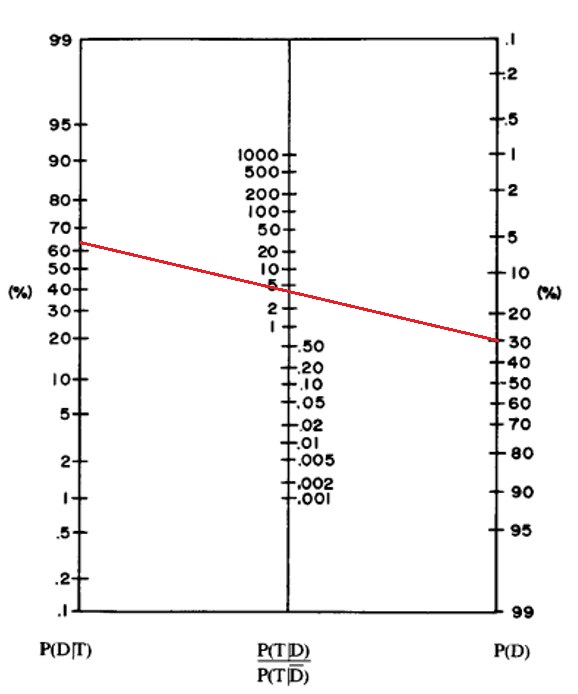
右側の軸のポイントを30%にして、中央の軸のポイントを陽性尤度比4.13(目分量)に置いて
両者を結ぶ直線を引くと・・・検査後の診断確率は63~65%の辺りになるかと思います。
計算によって求めた64%に近い値を目分量で確認する事ができます。
このように、Faganのノモグラムは計算の手間いらずで大まかな診断確率の変化を確認する事が可能となります。
検索すればノモグラムはたくさん見つかります。ただ、検査前後の軸の位置(左右)が違う事もあるので注意して下さい。
しかし、「ノモグラムを使う事すら面倒くさい」という方もいらっしゃるかと思います。
そんな方のために、尤度比の値が持つ意味合いをザックリと示した表があります。
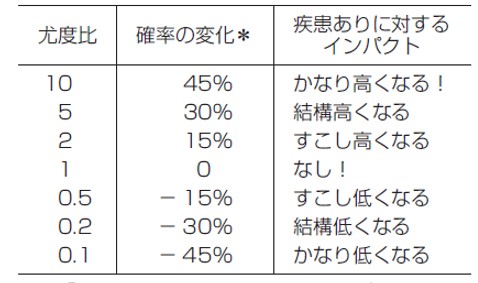
著者の方が、他の論文を元に作成した尤度比・検査前後の確率の変化・インパクト(印象)をまとめて表にしています。
例えば、尤度比5の行を見てみると30%となっています。
これは、陽性尤度比5の検査で陽性だったら、だいたい30%くらい診断確定の確率が上がるよ。という事です。
基本的に、この表の確率の変化が当てはまるのは検査前の診断確率が50%前後の場合です。
検査前の診断確率が90%近く高くなってきたり、逆に10%近く低くなると、表中の確率の変化は当てはまりません。
あくまでも、ザックリと尤度比の意味合いを掴むために利用してみると良いのではないでしょうか?
診断オッズ比に関して
※この項目は頭が混乱しやすいので、キツイ人は読み飛ばしてください!私はキツイです苦笑
尤度比は確率の比をみている。と考える事も出来ます。このような確率の比の事を「オッズ(odds)」と呼ぶこともあります。
ある出来事が起こる確率をPとすると、オッズと確率(P)の間には次のような関係があります。
オッズ =出来事の起こる確率/起こらない確率= P /(1 - P)
前回の投稿で的中度をリスクと考える事も出来るとお伝えしましたが、「リスク→割合(0~1の値をとる)」「オッズ→比(0~無限大)」と考えると少し頭の中が整理出来るかもしれません。
そして、このようなオッズを用いた比をオッズ比と言います。オッズ比→比の比となりますが・・・どんどん頭が混乱してきますね。
ここまでの考えを元にすると、今回求めた陽性尤度比・陰性尤度比から「診断オッズ比(diagnostic odds ratio:DOR)」を求める事も出来ます。
【DOR=+LR/-LR】しかし、その解釈は単純には考えられません。
診断オッズ比は、数値が大きいほど有効な検査と言えます。
しかし診断オッズ比が大きな値を取っていた場合、診断オッズ比だけでは+LRが大きいのか-LRが小さいのか分かりません。
確定診断に使える検査なのか、除外診断に使える検査なのか、DORは単独では判断材料にするのが難しい値だと私は感じています。
また、オッズという言葉が理解できると尤度比と検査前後のオッズの関係性も理解できます。両者には、以下のような関係性が成り立ちます。
検査前オッズ×尤度比=検査後オッズ
検査前オッズとは、検査を受ける前の状態における「疾患がある確率と疾患の無い確率の比」です。
検査後オッズとは、検査を受けて陽性となった状態における「疾患がある確率と疾患の無い確率の比」です。
もう、ついていくのが嫌になった人は丸覚えして下さい苦笑
以下に図示します。
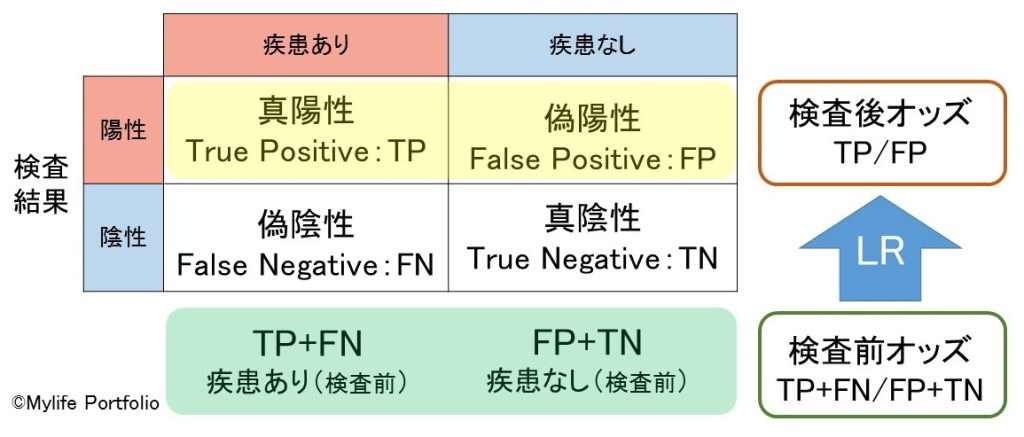
検査前後のオッズは「疾患の有無の比」のように見えるかもしれませんが、あくまでも検査結果の確率の比がオッズであり、数式が変形された結果「疾患の有無の比」のように考える事も出来るという事です。
上の表の考え方から尤度比を求める数式を変形させていっても、前述した陽性尤度比=感度/(1-特異度)と同じ数式に行きつきます。
まず理解してほしいのは、オッズ(比)と確率(割合)は裏表のような存在だという事
そして、尤度比は検査前後のオッズを左右する値だからこそ、先ほどのモノグラムのように検査の診断確率を求める使い方が可能となります。
この項目、決して蛇足ではないのですが、私自身の力量不足で非常に難解な話となってしまいました。
ここで混乱させてしまった方、どうもスミマセンでした。
とりあえず診断検査の分野に限れば、感度・特異度・尤度比が理解出来れば十分だと個人的には考えています。
しかし、オッズという言葉は診断検査以外の分野の研究でも出てくることがあります。
そのような他の分野に踏み込む時に備えて、オッズという言葉は頭の片隅に置いておくと良いかと思います。
さいごに
今回も引き続き診断検査についてまとめてみました。
前回と同じく、まずはPT/JSPO-ATは医学的な診断を下す事が出来る立場ではない事を留意しなくてはいけません。
ただ、診断検査に関する情報を正しく理解する事は大切だと私は考えています。
様々な数式は、ただ覚えて使っても支障は無いのかもしれません。
しかし私個人としては、理論背景を十分に理解したうえで様々な検査の情報を活用したいと思います。
あくまで私の頭の中の整理の為の投稿ですが、統計の分野は奥が深すぎて・・・自分自身も理解できているか度々不安になります苦笑
間違い等があるかもしれませんが、何か気付いた方は御指摘いただけると幸いです。


