前回のSALTAPSに関する投稿の中で、「リスク比」という言葉が出てきましたが、文中ではリスク比に関して簡単な説明のみで終わってしまいました。
実は、このリスク比という言葉を理解する為には「研究デザイン」に関する情報を整理しておく必要があります。
そこで今回は、研究デザインやリスク比について情報を整理していきたいと思います。
リスクとは?
リスク・リスク比について情報を整理する為に、1つ例題を考えてみましょう。
例題①:肺がんの患者1200名・肺がんでない人1880名を集め、過去5年間に継続した喫煙習慣があるか調査を実施した。
結果は以下の通りになりました。
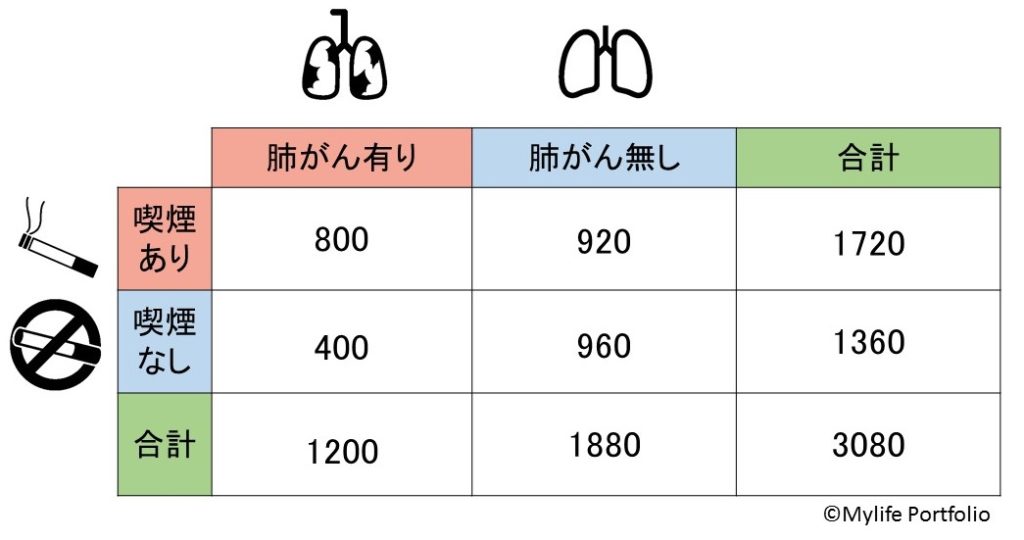
上記の結果から、「喫煙の有無と肺がんの関連」を調べる為にリスク比を求めてみましょう。
リスクとは「あるイベントの発生割合」の事です。
まず今回は喫煙あり/喫煙なしで肺がん発生に対するリスクを求めると、以下のようになります。
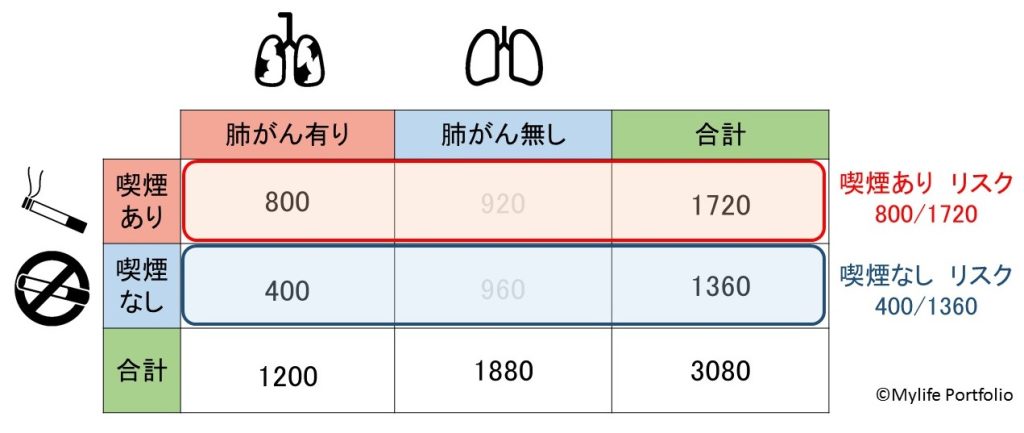
以前、診断検査に関する投稿の中で「的中度をリスクと考える事も出来る」と説明しましたが、的中度の求め方とリスクの求め方は同じです。(この考え方は後でも出てきますので、少し覚えておいて下さい)
今回のイベントは「肺がん」なので、喫煙あり群/喫煙ない群における肺がん患者の割合を求めるという流れになります。
次にリスク比を求めていきたいと思いますが、リスク比とは2群のリスクの比です。そのまんまです苦笑
上記の例でいえば、「喫煙あり群のリスク 800/1720」と「喫煙なし群のリスク 400/1360」の比なので
800/1720 ÷ 400/1360 となり、おおよそ1.58という値になります。
リスク比が1.0より大きいという事は、「喫煙あり群は、喫煙なし群より肺がんのリスクが1.58倍大きい」と考える事ができます。
・・・と、言いたいところなのですが
実は上記の流れでリスク比を求める事は適切なデータの分析とはいえません。
決して、リスク・リスク比に関する説明に間違いがあった訳ではありません。
結論を言うと、「今回の研究デザイン(ケース・コントロール研究)において、リスクを求めてはいけない」のです。
それは何故なのか?ここから研究デザインについて考えながら説明していきたいと思います。
「割合」と「比」という似た意味の言葉が出てきて、この時点で混乱してくる方もいらっしゃるかと思います。この二つの用語は以下の様に定義づけられています。
・比(rate)
ある量を別の量で割ったもの
・割合(proportion)比の一種,分母が分子を含んでいるもの
田中 司朗.京都大学大学院医学研究科 聴講コース 臨床研究者のための生物統計学 「リスクの指標と治療効果の指標」.講義資料より引用.
基本的に大きい概念としての「比」が存在し、その中で分母が分子を含んでいるものを割合と呼びます。
介入研究と観察研究
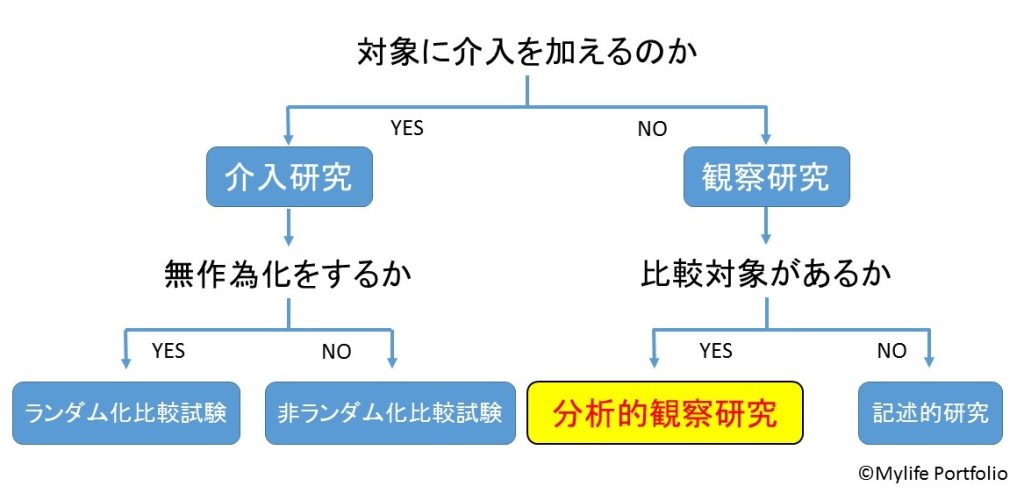
https://www.igaku-shoin.co.jp/paper/archive/y2019/PA03324_05 を参考に作図
まず、研究のデザインを考える上で「研究者が対象に介入を加えるかどうか」という区分けがあります。
上の例題で挙げたような、研究者が対象(被験者)に介入を加えない調査を「観察研究」と呼びます。
特に今回の例題(喫煙あり / 喫煙なし)のように群間で比較する場合は、分析的観察研究と呼ばれます。また、観察研究でも比較対象のない、症例報告(珍しい病気などの患者がいた場合、その情報をまとめて報告)のような研究手法を記述的研究と呼びます。
一方、観察研究とは逆に対象に介入(薬の投薬やトレーニングの実施など)を加える調査を介入研究と呼びます。介入研究は、対象者に介入を加えるグループ(介入群)と介入を加えないグループ(コントロール群)を設ける場合が多く、その群分けを無作為化(ランダムに群分け)するかどうかで、更に区分けが異なります。
実際には他にも細かい分類がありますが割愛させていただきます。次に、この分析的観察研究について詳しく説明してきたいと思います。
横断研究と縦断研究
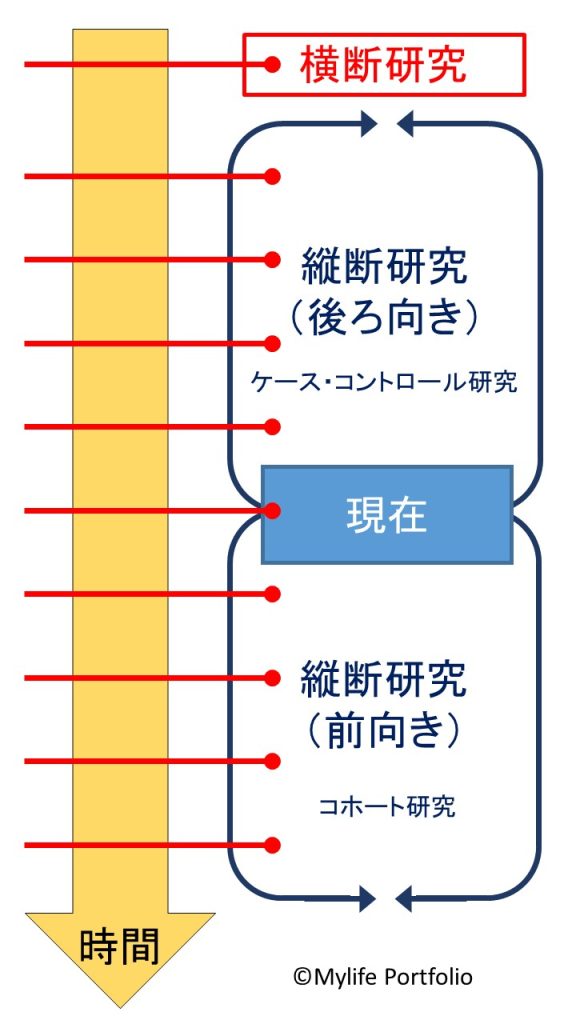
分析的観察研究には、時間の経過と合わせて「横断研究」と「縦断研究に」分かれます。
ある一時点において、原因と結果を同時に調査する研究が横断研究
時間を追って、原因と結果を異なる時点で調査する研究が縦断研究です。
また縦断研究は、時間軸の方向(原因と結果)によって更に「ケース・コントロール研究」と「コホート研究」に分かれます。
ケースコントロール研究は結果から原因にさかのぼって関連をみる研究で,典型的にはある時点で疾患を有する患者さんと対照群について,過去の何らかの暴露因子(あるいは患者背景や治療介入)の有無について調査します.
神田善伸. みんなのEBMと臨床研究. p70. 南江堂. 2016年
疾患を有する患者がケース・対照群をコントロールと呼ぶので、ケース・コントロール研究と呼ばれています。
しかし字面だと分かりにくいので、先ほどの例題を元に図示してみます。
例題①:肺がんの患者1200名・肺がんでない人1880名を集め、過去5年間に継続した喫煙習慣があるか調査を実施した。
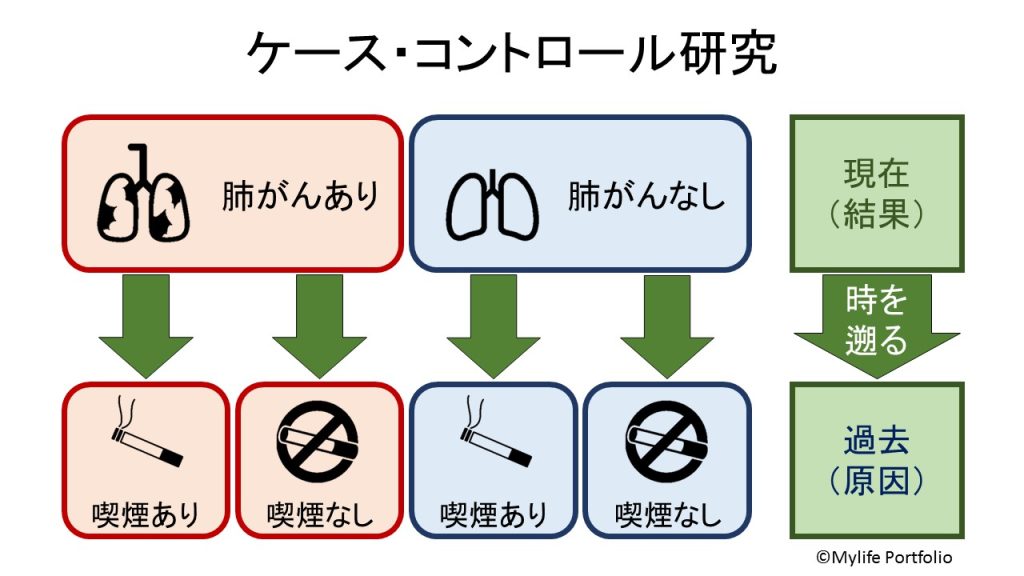
今回の例題のように現在(結果)から過去(原因)に時間軸を後ろ向きに遡って関連をみる研究は、ケース・コントロール研究だといえます。
一方、コホート研究とはどのような縦断研究なのでしょうか?
コホート研究は原因から結果への方向で関連をみる研究で,たとえばある時点で暴露因子(あるいは患者背景や特定の治療)のある群とない群について,その後の疾患の発症(あるいは何らかの結果の発生)の有無を調査するものです.
神田善伸. みんなのEBMと臨床研究. p70. 南江堂. 2016年
コホート研究に関しては、別の例題を上げて図示してみたいと思います。
例題②:喫煙習慣のある1万人・喫煙習慣のない1万人を集め、肺がん発症の有無を5年間追跡調査した。
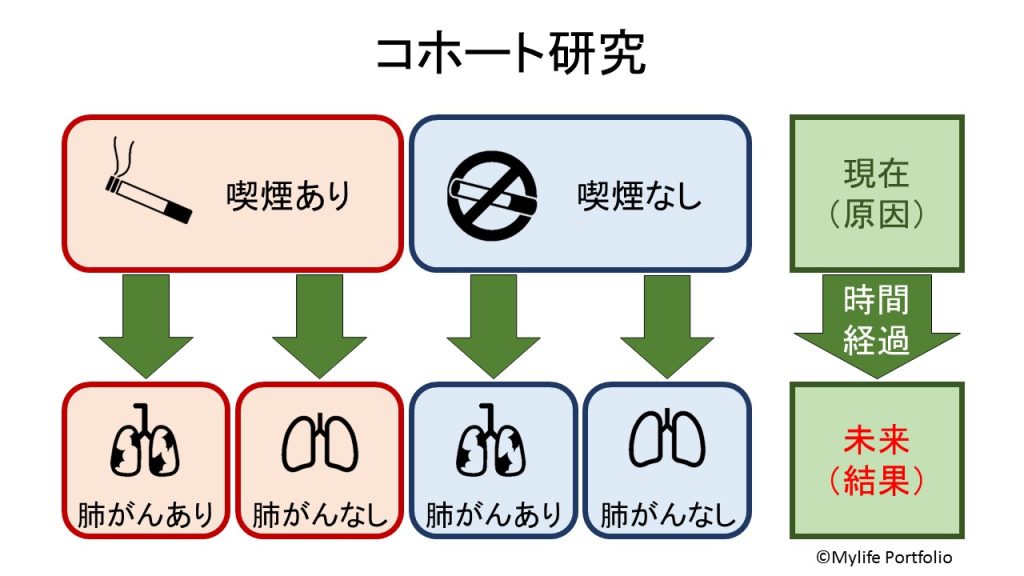
コホート研究は、現在(原因)から未来(結果)に向けて時間軸を前向きに進み関連をみる研究だといえます。
実際にはコホート研究(原因→結果)の中でも、「現在の原因」ではなく「過去の原因」と「現在(若しくは未来)の結果」を調べるコホート研究の事をヒストリカルコホート研究と呼びます。
例)過去に特定の治療を行った患者が、現在どのような状態なのか調査を実施する
もちろん時系列は大切なのですが、今回は「コホート研究」と「ケース・コントロール研究」の違いが重要となります。頭が混乱しない様に、各研究デザインにおいてどのように原因と結果の関係を捉えているのか注意して下さい。
ケース・コントロール研究 VS コホート研究
ケース・コントロール研究およびコホート研究には、それぞれ一長一短があります。
例えば今回例に挙げた肺がんのような疾患の場合、コホート研究を実施する事は大変です。
国立研究開発法人国立がん研究センターの情報によると2018年における日本の肺がんの人口あたり罹患率は10万人に対して97.1 例でした。(https://ganjoho.jp/reg_stat/statistics/stat/cancer/12_lung.html 2022年4月16日参照)
このように発生が稀な疾患においてコホート研究を行おうとすると、患者数を確保する為に数千人では済まない被験者が必要となります。
一方で、ケース・コントロール研究の場合は「まず最初に患者を集めてしまう」ため、コホート研究のように大勢の被験者を必要としません。
この点だけを考えると、研究に費やせるマンパワーや資金の問題から、多くの被験者を必要としない手軽なケース・コントロール研究の方が実施しやすいといえます。しかし、ケース・コントロール研究にも欠点があります。
まずは、暴露因子について考えてみましょう。
例題では「喫煙習慣と肺がんの関係」を調べていますが、この喫煙習慣が暴露因子となります。
では、「1本5000円以上する葉巻の喫煙習慣と肺がんの関係」を調べる場合はどうでしょうか?

ケース・コントロール研究として、肺がんの患者と対照群(健康な人)を集めたとしても「超高級な葉巻を日常的に吸っている」ような人間が数多く含まれているとは思えません苦笑
被験者数を稼ごうとして、超高級葉巻を吸っている人を探し出そうとしてしまえばデータの偏り(バイアス)を引き起こしてしまいます。
このように、ケース・コントロール研究は、稀な暴露因子について調査する事が難しいという欠点があります。
また、ケース・コントロール研究の欠点は他にもあります。それが、今回のテーマである「ケース・コントロール研究において、リスクを求めてはいけない」という話に繋がっていきます。
観察研究におけるリスク比とオッズ比
コホート研究におけるリスク比とオッズ比
では、今回取り上げている例題を元にリスク比とオッズ比について説明していきたいと思います。
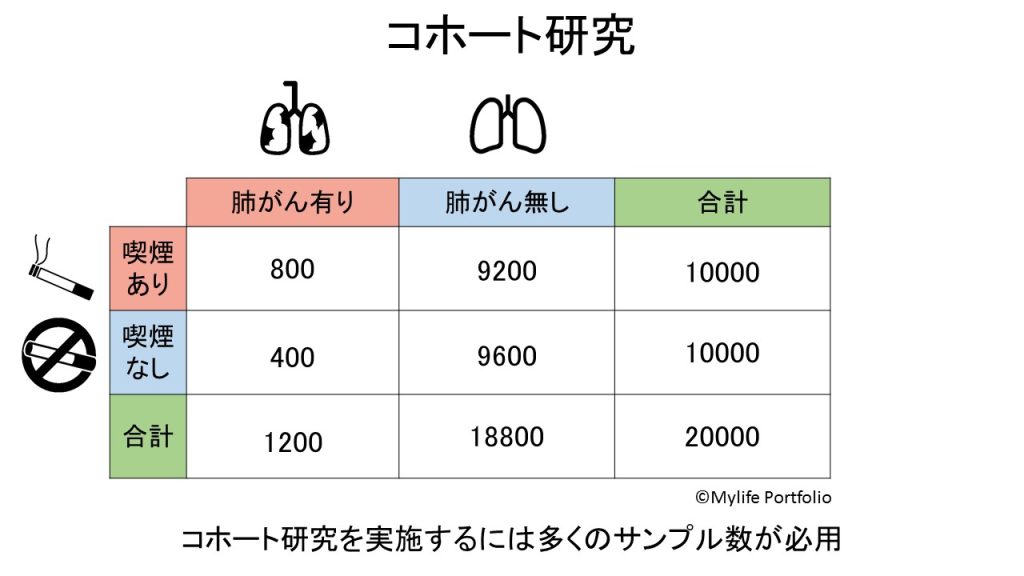
例題②:喫煙習慣のある1万人・喫煙習慣のない1万人を集め、肺がん発症の有無を5年間追跡調査した。
調査の結果を以下に示します。
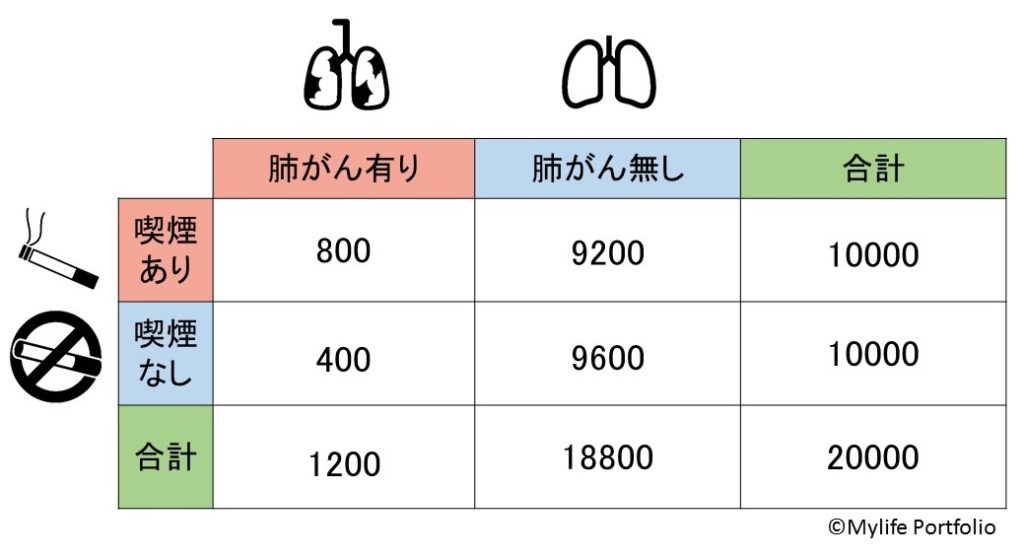
では、まずリスク比を求めてみましょう。リスク比はイベントの発生割合であるリスクの比の事です。今回のイベントは肺がんの発症なのでリスクは以下のように求められます。
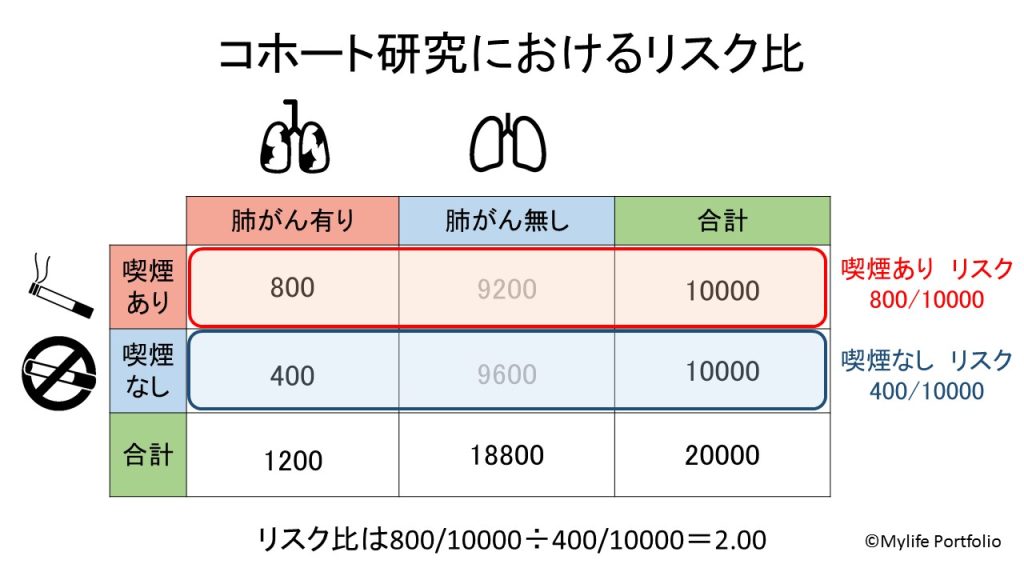
リスク比が2.00という事は、喫煙あり群の方がリスク(肺がんを発症する割合)が2倍である。という事になります。
では、次にオッズ比について説明していきます。
そもそもオッズとは「ある出来事の発生する確率 / 発生しない確率」から求められます。
コホート研究では原因(喫煙)から結果(肺がん)を調査しているので、コホート研究におけるオッズは結果(肺がん)の確率を元に求めます。
喫煙あり群のオッズは800/10000÷9200/10000=800/9200となり
喫煙なし群のオッズは400/10000÷9600/10000=400/9600となります。
そこから、2群のオッズの比であるオッズ比を求めていきます。
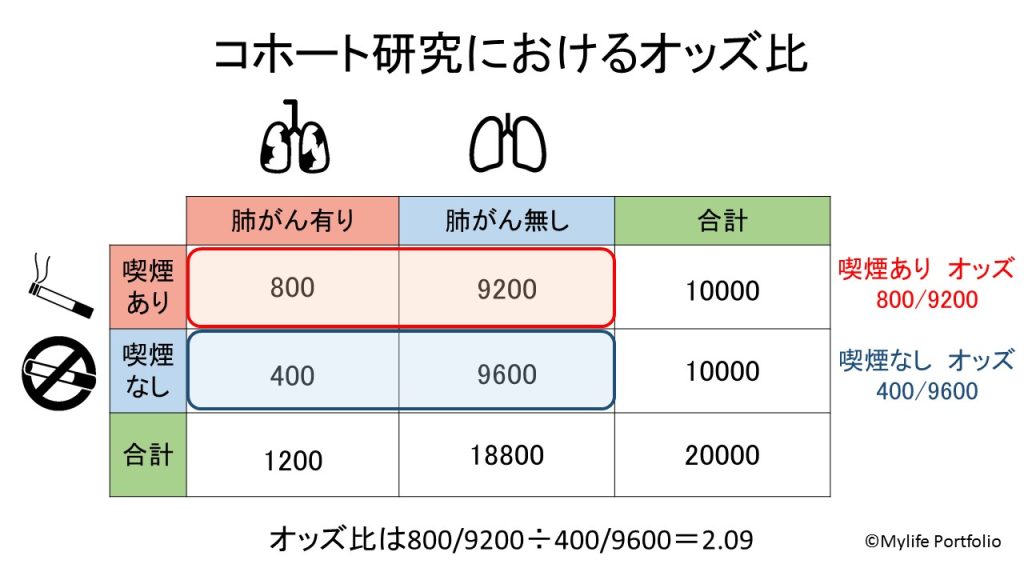
オッズ比は2.09という値が求められました。
・・・で、どうゆう事なの?という疑問が沸いてくるかと思います。私も「オッズ比って何なの?」と質問されたら上手く答えられません苦笑
ここで重要なのは、オッズ比(2.09)とリスク比(2.00)が近い値をとっているという事です。
発生が稀なイベントを調査するコホート研究において、オッズ比はリスク比と近似値をとるという事が重要なポイントです。
いやいや、リスク比を求めればいいんだから、わざわざオッズ比を求める必要ないじゃないか。と考えられると思いますが、確かにコホート研究においてオッズ比を求める必要性は高くありません。
しかしケース・コントロール研究では、このリスク比がアテにならなくなってしまうので、オッズ比が重要となってきます。
ケース・コントロール研究におけるリスク比とオッズ比
先ほどの例題では、コホート研究を行う為に2万人の被験者を集めてきました。しかし、このような大規模な研究を実施できなかった為にケース・コントロール研究を実施したとしましょう。
例題①:肺がんの患者1200名・肺がんでない人1880名を集め、過去5年間に継続した喫煙習慣があるか調査を実施した。
ここで、最初の例題に戻ってきます。先ほどの例題②と同じ母集団から肺がんの患者1200名集め、肺がんでない18800名の中から1880名をランダムに選びだしたとしましょう。
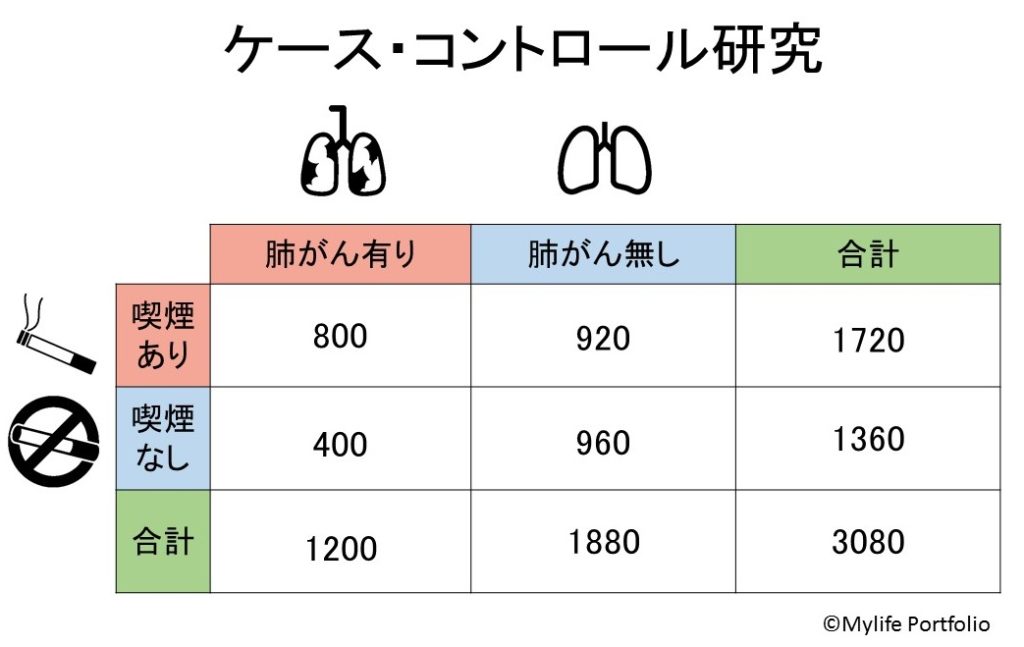
では、コホート研究の時と同様にリスク比を求めてみたいと思います。

リスク比を計算で求めると1.58となりました。あれ?先ほどのコホート研究ではリスク比は2.00だったのに、どうして値が違うのでしょうか?
今回の研究は先ほどのコホート研究と同じ母集団からデータを取っています。しかし、今回の研究では疾患が稀な肺がんを扱っている為に、ランダムサンプリングにより肺がん無し群の被験者数が減っています。
この為、コホート研究からケースコントロール研究にデザインを変更した事で、肺がんの有病率が変化し、リスク値も同様に変化してしまいました。
これは、診断検査において的中度が有病率に左右されるのと同じ原理です。何となく話が繋がってきたでしょうか?(詳しくは以前の投稿を御参照下さい)
このような理由から、ケース・コントロール研究においてリスクを求めてはいけない(リスクが正しく反映されていない)という考えに至ります。
では、どうしたら良いのでしょうか?ここで、ケース・コントロール研究におけるオッズ比が必用となってきます。
再度確認しますが、オッズとは「ある出来事の発生する確率 / 発生しない確率」から求められます。
ケース・コントロール研究では結果(肺がん)から原因(喫煙)を調査しているので、ケース・コントロール研究のオッズは 原因(喫煙)の確率を元に求めます。
肺がんあり群のオッズは800/1200÷400/1200=800/400となり
肺がんなし群のオッズは920/1880÷960/1880=920/960となります。
そこから、2群のオッズの比であるオッズ比を求めていきます。

計算の結果、ケース・コントロール研究におけるオッズ比は2.09とコホート研究と同じ値となりました。
詳しい原理や証明は割愛しますが、母集団が同じであればケース・コントロール研究におけるオッズ比とコホート研究におけるオッズ比は等しい値をとります。
またコホート研究におけるオッズ比はリスク比と近い値をとる為、ケース・コントロール研究では、オッズ比を求める事で真のリスク(コホート研究のリスク)を推定する事が出来るという事になります。
オッズ比は、ケース・コントロール研究の欠点を補うためにある。と考える事も出来ます。
まとめ
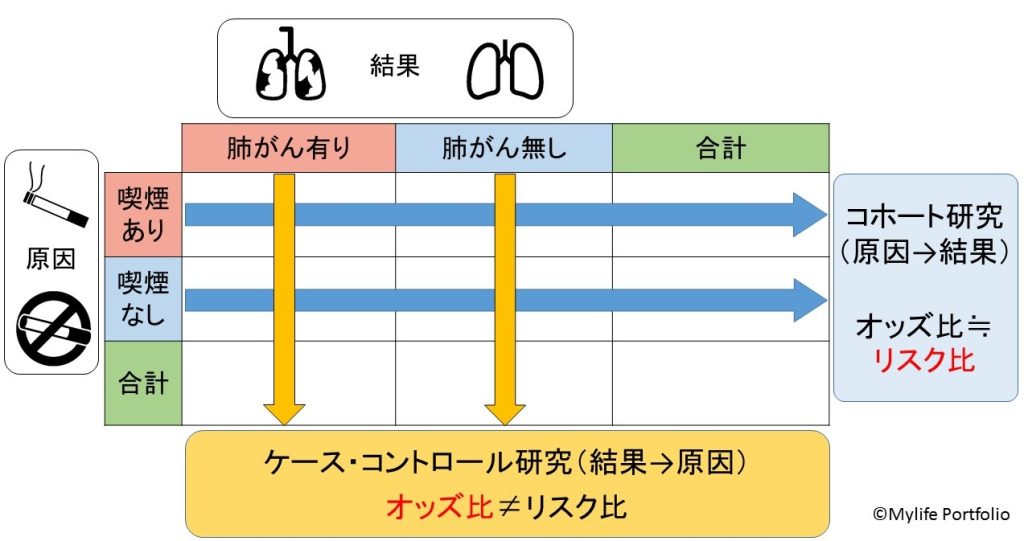
ここまでの内容で、最初に述べた「ケース・コントロール研究においてリスクを求めてはいけない」という事が少しでも理解いただければ幸いです。
このケース・コントロール研究の欠点を補うのが「オッズ比」となります。しかし、オッズ比は「何の確立に対するオッズなのか?」を理解しなければ、不適切な計算方法でオッズを求めてしまう可能性があります。
・コホート研究では原因から結果を見ているので、結果に関するオッズを求める
・ケース・コントロール研究では結果から原因を求めているので、原因に関するオッズを求める
という上記の流れを理解してオッズ比を求める事が出来れば、ケース・コントロール研究の結果を正しく理解できるはずです。
上の図表に有る様に視覚的にイメージできれば、それぞれの研究デザインにおけるオッズの計算方法も頭に浮かびやすいかと思います。
今回の例題や図表は、千葉康敬「医療統計力」を鍛える!P148-163. 総合医学社. 2015年 を参考に作成させて頂きました。
また、以下の書籍の内容も引用させて頂きました。今回の研究デザインに関する内容以外にも幅広くEBMに関わる内容が取り上げられていますので、興味がある方は是非一度ご覧になってみて下さい。
さいごに
私は大規模なコホート研究に携わるような立場ではなく、ケース・コントロール研究に臨む事が多くありました。しかし、ケース・コントロール研究とリスクに関する知識を十分に整理できないまま、調査にあたっていた事もありました。
このような知識は学生時代にも触れる機会はありましたが、やはり自分自身が研究に関わる事で初めて重要性を実感しました。
今回の投稿も、多くの方にとっては小難しくて退屈な内容だったかと思います。しかし、今はこのような知識に重要性を感じなかった方も、いつの日か今回の知識が必要になるかもしれません。
その時に、この投稿が少しでもお役に立てば幸いです。



