この検査、誰が行っても結果は一緒？【級内相関係数 / Kappa値】

前回の投稿から長らく間があいてしまいました苦笑

前回SALTAPSについてまとめていく中で、関節可動域の測定に関する研究を紹介しました。

測定者が異なる場合でも、同じような測定結果が得られるのかを調べた研究ですが、そこでは級内相関係数（Intraclass correlation coefficients：ICC）という言葉が出てきました。

級内相関係数とは検査の信頼性を示す為の指標です。

そのまま放置して次に進むのは少し気になるので、今回は検査の信頼性を調べる方法について情報を整理してみたいと思います。

検査の信頼性と妥当性

そもそも、様々な検査法や尺度が優れたものであるかどうか考える上で「信頼性」と「妥当性」という観点が重要になってきます。

信頼性と妥当性とは、（研究・検査に関する場面で）どのような意味を持つ言葉なのでしょうか？

測定の信頼性とは、全ての条件が同じ時の測定の一貫性として定義されます。

（～中略～）

妥当性は操作的定義のところでも触れたように、測定の理論的合理性、すなわち測定方法が測定しようとするものをどの程度反映しているかを示すものとして定義されます。
谷浩明. 信頼性と妥当性について. 理学療法のための運動生理. 5 巻 3 号p. 119-125. 1990年

なかなか、文章で理解しようとしても難しいものがあります苦笑

このような信頼性と妥当性をイメージしやすく説明してくれる「ダーツのアナロジー」呼ばれる考え方があります。

今からあなたが的に向かってダーツを投げるとしましょう。「ダーツの矢」が検査、「的の中心」が検査で測定したい目的だとしましょう。

さて、とりあえずダーツを投げてみると下の図の様な結果になりました。

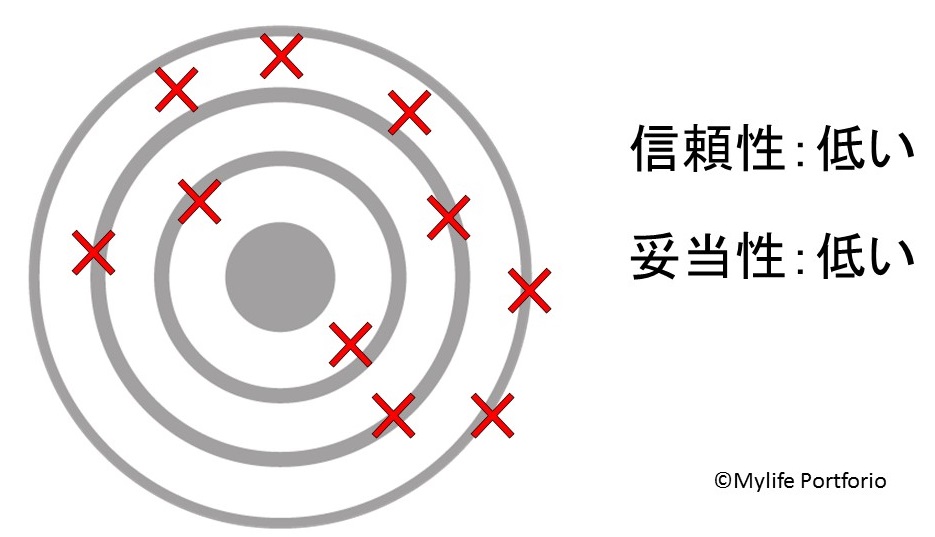
ダーツの刺さった場所は、てんでバラバラ。的の中心を捉えているようにも思えません。

このような状態はダーツ（検査）の信頼性も妥当性も共に低いと言えるのですが、この例だけでは良く分からないと思いますので、もう一度ダーツを投げてみましょう。

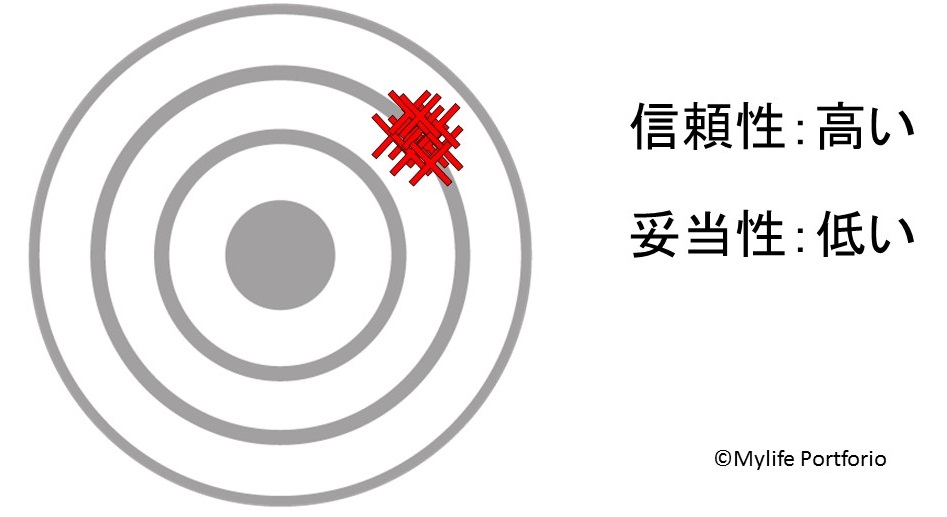
おお！今度は先ほどと比べて良い感じではないでしょうか？ダーツのバラつきが小さくなりました。

このように結果のバラつきが小さい場合、検査の信頼性が高いと考える事ができます。

しかし「的の中心を狙う」というダーツのゲームの目的から考えると、今回の結果では高い得点は得られないでしょう。

つまり、ダーツ（検査）の結果が的の中心（検査の目的）からズレているのです。このような場合は、検査の妥当性が低いと考えられます。

例えば、「全身の柔軟性」を明らかにする為に「体重」を測ったとしましょう。

おそらく、正しく体重計を使用すればデータは大きくバラつく事はないので「体重の測定」自体は信頼性の高い検査だと考えられます。

しかし、体重そのものと「全身の柔軟性」の間には強い関連はみられないはずです。

「全身の柔軟性」を「体重の測定」で検査しようとするのは、文字通り的外れで妥当性が低いという事です。

例えば体育の授業で行った長座体前屈など、柔軟性を測定するための検査法は存在します。

もしかしたら、身体が小さく体重の軽い子供の方が体重の重たい大人より柔軟性が高いかもしれません。

このような場合は、体重と全身の柔軟性（長座体前屈）の結果の間に統計的な関係性が認められるかもしれませんが、直接的な関連はないはずです。

では、信頼性も妥当性も優れた検査であればダーツの矢はどのように的を捉えるのでしょうか？

優れた検査法であれば、上の結果のように結果のバラつきも小さく（信頼性が高い）結果自体も的の中心を捉えている（妥当性が高い）はずです。

そして、ここから先の話では「検査の信頼性」をどのように評価するのか？という点に着目していきます。

2種類の信頼性

いよいよ今回の投稿の本題である、検査法の信頼性について考えていきたいと思います。

先ほどのダーツのアナロジーを通して、信頼性とは測定結果の一貫性だという事が理解できたかと思います。

検査における信頼性には、大きく2つの種類が存在します。例えば、腕の筋肉の太さを評価する為に腕の周径をメジャーで測定するとしましょう。

1人の検者が行う検査結果に一貫性があるのかを表しているのが「検者内信頼性」です。

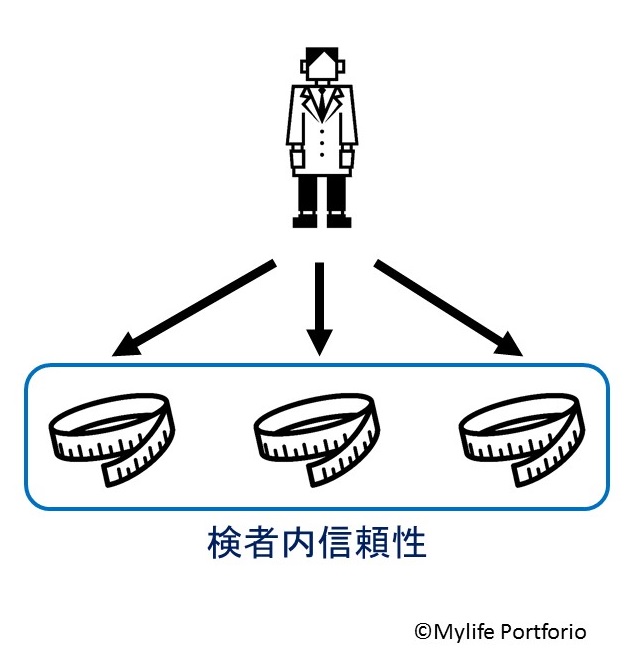
一方、複数の検者がそれぞれ行った検査結果に一貫性があるのかを表しているのが「検者間信頼性」となります。

なんとなくイメージできたでしょうか？　このような検者内信頼性や検者間信頼性を示す為の指標が級内相関係数となります。

級内相関係数とは

級内相関係数(ICC)とは、分散分析を元に求められる指標です。

詳しい計算方法は割愛しますが、簡単に説明するとICC=真値の分散/全体の分散と考える事ができます。（今井樹. 理学療法研究における”評価の信頼性”の検査法. 理学療法学. 19巻3号p262. 2004）

ICCは0～1.0の値をとります。真値の分散の値と全体の分散が等しければICCは1.0となります。

実際にICCがどれだけ大きければ、信頼性が高いのか？と気になるかと思います。

ICCが0.61以上はsubstantialである、0.7以上はOKなどといった慣習的な基準を見かける事はありますが、少なくとも現時点（2022年5月25日）で理論的に説明した報告等を私は見つける事が出来ませんでした。

数値の解釈は、自身の研究分野の先行研究等を参考にする必要があると思いますが、その点に関しては今回議論はしないでおきます。

本題に戻りますが、ICCを求める方法は大きく分けて6種類存在します。それぞれ例を挙げて説明したいと思います。

ICC(1，1)およびICC(1，ｋ)

ICC(1，1)とICC(1，ｋ)は検者内信頼性を求める際に使用されます。

ICC(1，1)は1人の検者が複数回の測定を行った結果の信頼性を求め、ICC(1，ｋ)は測定の結果の平均値から信頼性を求めます。

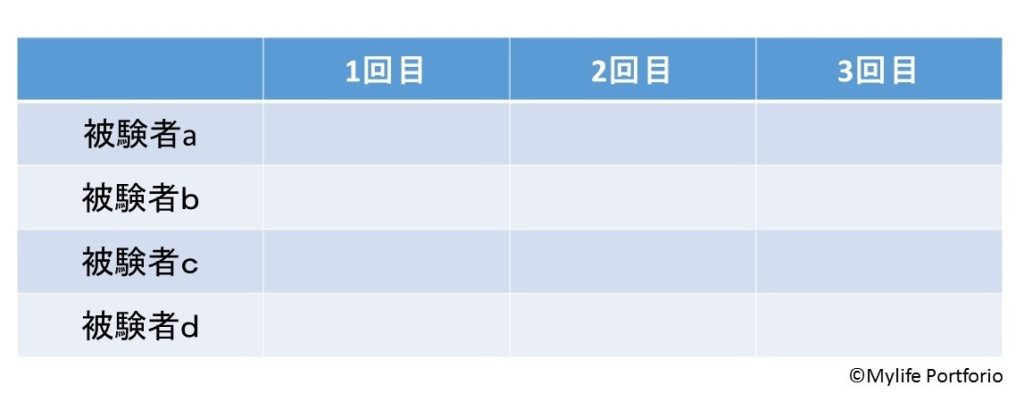
例えば、上のようなケース。1人の検者が4人の被験者に対し、それぞれ3回の測定を行った場合を考えます。

・全12回それぞれの値の分散から求められる級内相関係数はICC(1，1)

・各3回の測定の平均値の分散から求められる級内相関係数はICC(1，k) → 今回の場合はICC(1，3)

となります。

ICC(2，1)およびICC(2，ｋ)

ICC(2，1)とICC(2，ｋ)は検者間信頼性を求める際に使用されます。

ICC(2，1)は複数人の検者が測定を行った結果の信頼性を求め、ICC(2，ｋ)は測定の結果の平均値から信頼性を求めます。

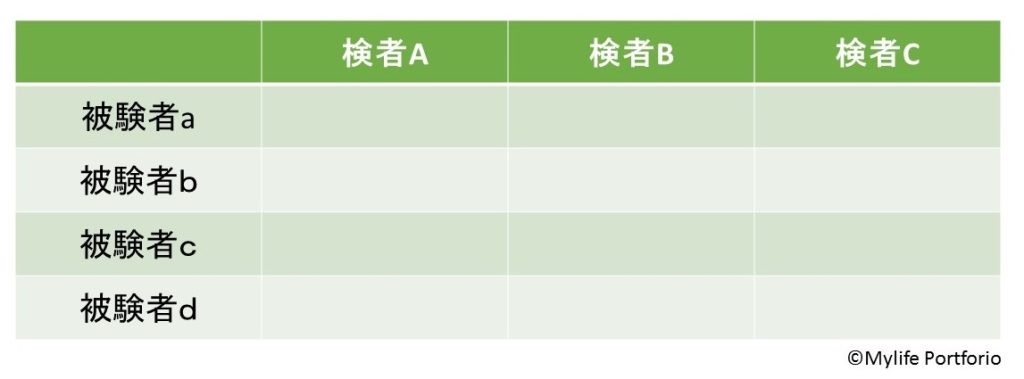
例えば、上のようなケース。3人の検者が4人の被験者に対し、それぞれ測定を行った場合を考えます。

全12回それぞれの値の分散から求められる級内相関係数はICC(2，1)となります。

次にICC(2，ｋ)を考える為に少し異なるケースを考えてみます。

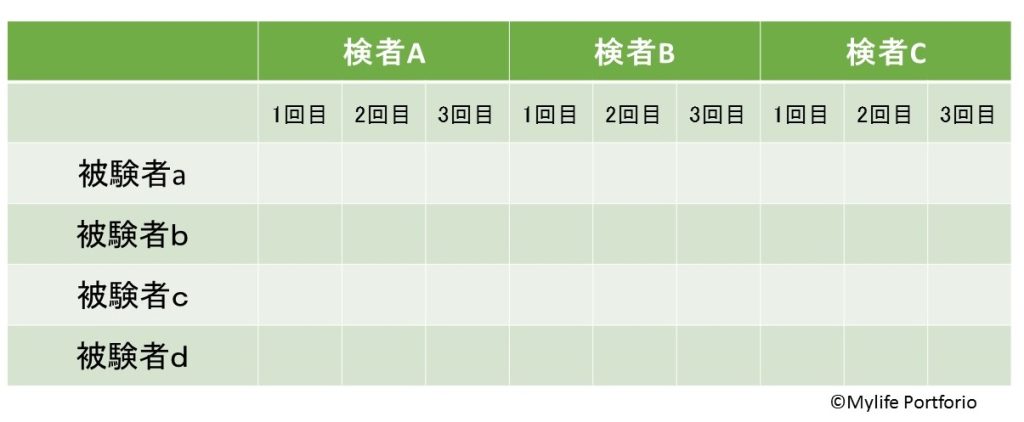
今度は3人の検者が4人の被験者に対し、それぞれ3回ずつ測定を行った場合を考えます。

各3回の測定の平均値の分散から求められる級内相関係数はICC(2，k) → 今回の場合はICC(2，3)となります。

ICC(3，1)およびICC(3，ｋ)

ICC(3，1)とICC(3，ｋ)はICC(2，1)・ICC(2，ｋ)と同様に検者間信頼性を求める際に使用されます。

両者の違いは、ICC(2，1)・ICC(2，ｋ)が絶対的な一致を調べるもので、ICC(3，1)・ICC(3，ｋ)が相対的な一致を調べるものであるという点です。

絶対的な一致と相対的な一致とは、どのような事でしょうか？

ここで、インピーダンス法による体脂肪率の測定を例に挙げて考えてみたいと思います。

体内に微弱な電流を流す事で体脂肪率などを推定するインピーダンス法は、家庭用の体組成計などで手軽に実施できる測定方法です。

しかし、電流から体脂肪率を推定する方法（計算式など）は製品メーカーによって微妙に異なります。

もしかしたら、あるメーカーの製品は正しい値より常に高めの数値が出てしまったり、逆に正しい値より常に小さい値が出てしまうかもしれません。

このような場合、各メーカーの数値は一致しないのでICC(2，1)で求められる値は小さくなり信頼性は低くなると考えられます。これが絶対的な一致をみているという事です。

しかし、常に数値が高く(小さく)なったとしても、「体脂肪の割合が高い人を体脂肪率が高い」「体脂肪の割合が小さい人を体脂肪率が小さい」と正しく測定できており、各メーカー製品の測定結果が相対的（平行）であれば、相対的な一致度は高いと言えます。

現に、測定機器によって体脂肪率の値が変わる事はスポーツ現場のフィットネスチェックでも起こりえます。

検査の絶対的な一致度が低く、検査毎に値がバラつくと選手やサポートスタッフも混乱しますが、体脂肪率の測定自体の相対的な一致度が高い事を理解できていれば

「同じ測定機器で変化を追っていけば、体脂肪率の変化を正しく終える事が出来る」と測定結果に振り回される事もないはずです。

このような相対的な一致を調べた指標がICC(3，1)やICC(3，ｋ)となります。

ICCを正しく使う

ここまで説明したICCの6つのパターンに関して、気を付けないといけない事があります。

当たり前ですが、正しい方法でICCを求める事。ICCはデータさえあれば間違った方法を選んでしまっても結果は出てきます。

研究デザインと統計手法が合っていない場合、実際よりもICCを高く見積もってしまったり低く見積もってしまう事になるかもしれません。

自分自身が解析を行う際に注意するのはもちろんですが、研究論文の中で統計手法を目にする際にも注意しなくてはいけません。

時折、「あれ？何で複数の検者で相関係数求めているのにICC（1，1）なのだろう」といった論文を目にする事もあります。

そこに研究者自身の理由付けがあり、かつ納得できるものであれば良いのですが･･･

多くの研究者がお世話になっているであろう様々な統計ソフトは「クリックひとつ」で統計の計算結果を求める事が出来るので、結構間違いも多いのではないかと思います。

私は度々統計手法間違えてしまい、研究室の教授に指摘されて気付く事が多々ありました。

私の様な者は少ないかもしれませんが苦笑、意外と統計手法に関して疑問点を抱く論文に出会う事も多い、というのが私の印象です。

ICCが使えない場合（カッパ統計量）

ここまで級内相関係数（ICC）について説明してきました。最初に述べたようにICCは分散分析を元に求められる指標なので、適応には条件があります。

・正規分布に従うデータであること．
・比率尺度か間隔尺度，または一部例外として段階数の多い順序尺度のデータ．
対馬栄輝. SPSSで学ぶ医療系データ解析. 第7刷. 東京図書. ｐ195. 2011

ここで、正規分布やデータの尺度に関する説明を始めると大変なので苦笑

ザックリ説明すると、測定結果が「数字の差に意味がない」「数字の大小にしか意味がない」といった場合、「そもそも数値で結果が表せない」場合はICCを求める事は出来ません。

例えば、血液検査を実施して血液型を判定するような場合を考えてみましょう。検査の結果は「A型」「B型」といった数値で表されるものではない為、ICCを求める事は出来ません。

このような場合は、ICCではなくカッパ統計値（kappa statistic）という値を求めます。カッパ統計量は ICCと同様に0～1.0の値をとり、検査の結果が完全に一致する場合は1.0となります。

詳しい計算方法は割愛しますが、興味がある方は御自分で調べてみて下さい。

今回引用したり、参考にさせてもらった書籍を紹介しておきます。